Idź do:
1
2
3
4
5
6
7
8
9
Matura podstawowa - kurs - część 12 - zadania
Funkcja liniowa - praktyczny sposób na rysowanie wykresu
Na filmie pokazuję praktyczną metodę na szybkie rysowanie dokładnych wykresów funkcji liniowych.
Zadanie 1. (1 pkt)
Na jednym z poniższych rysunków przedstawiono interpretację geometryczną układu równań {x+3y=−53x−2y=−4 Wskaż ten rysunek.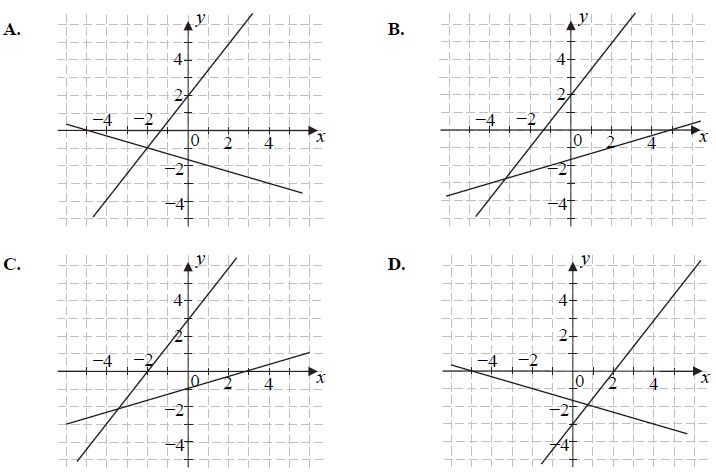 
Odpowiedź: A
Matura 2017
Zadanie 2. (1 pkt)
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.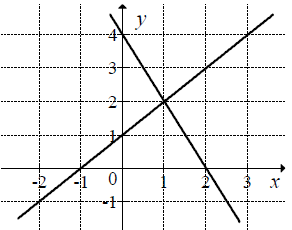 
Wskaż ten układ.
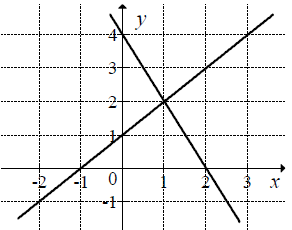Wskaż ten układ. A. {y=x−1y=−2x+4
B. {y=x−1y=2x+4
C. {y=x+1y=−2x+4
D. {y=x+1y=2x+4
Odpowiedź: C
Matura 2017
Zadanie 3. (1 pkt)
Interpretację geometryczną układu równań {x−y=2−2x+2y=4 przedstawiono na rysunku: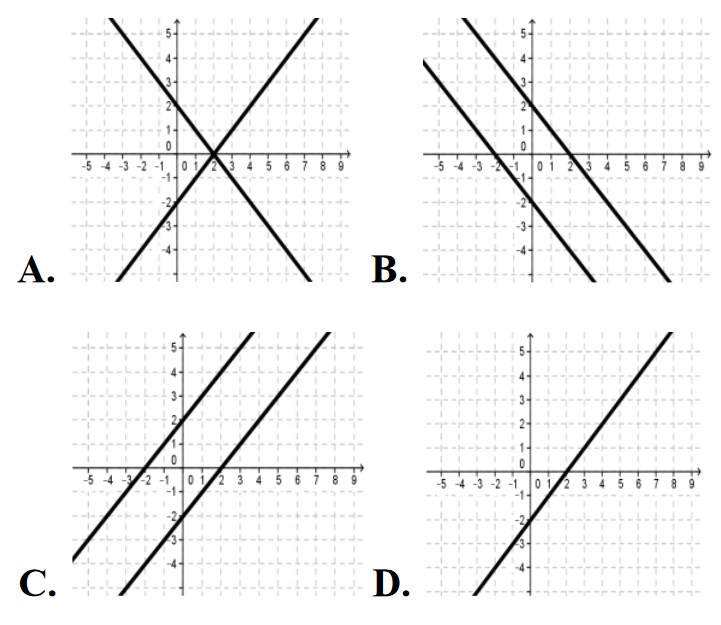 
Odpowiedź: C
Matura 2017
Zadanie 4. (1 pkt)
Układ równań {y=3x+2y=(m−2)x+5 nie ma rozwiązań, gdy
A. m=2
B. m=3
C. m=4
D. m=5
Odpowiedź: D
Matura 2017
Zadanie 5. (1 pkt)
Układ równań {x−y=32x+0,5y=4 opisuje w układzie współrzędnych na płaszczyźnie
A. zbiór nieskończony.
B. dokładnie 2 różne punkty.
C. dokładnie jeden punkt.
D. zbiór pusty.
Odpowiedź: C
Matura 2017
Zadanie 6. (2 pkt)
Rozwiąż układ równań {x+3y=52x−y=3 .
Odpowiedź: \(\begin{cases} x=2 \\ y=1 \end{cases} \)
Matura 2017
Zadanie 7. (1 pkt)
Układ równań {4x+2y=106x+ay=15 ma nieskończenie wiele rozwiązań, jeśli
A. a=−1
B. a=0
C. a=2
D. a=3
Odpowiedź: D
Matura 2017
Zadanie 8. (1 pkt)
Rozwiązaniem układu równań {3x−5y=02x−y=14 jest para liczb (x,y) takich, że
A. x<0 iy<0
B. x<0 iy>0
C. x>0 iy<0
D. x>0 iy>0
Odpowiedź: D
Matura 2017