Idź do:
2
4
6
8
10
12
Matura podstawowa - kurs - część 27 - zadania
Zadanie 1. (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f . 
Funkcja f określona jest wzorem
Funkcja A. f(x)=−12(x−3)(x+1)
B. f(x)=12(x−3)(x+1)
C. f(x)=−12(x+3)(x−1)
D. f(x)=12(x+3)(x−1)
Matura 2017
Zadanie 2. (1 pkt)
Parabola o wierzchołku W=(−3,5) i ramionach skierowanych w dół może być wykresem funkcji określonej wzorem
A. y=2⋅(x+3)2+5
B. y=−2⋅(x−3)2+5
C. y=−2⋅(x+3)2+5
D. y=−2⋅(x−3)2−5
Matura 2017
Zadanie 3. (1 pkt)
Funkcja kwadratowa, której zbiorem wartości jest przedział (−∞,−3⟩ , może być określona wzorem
A. y=(x+2)2−3
B. y=−(x+3)2
C. y=−(x−2)2−3
D. y=−x2+3
Matura 2017
Zadanie 4. (1 pkt)
Funkcja kwadratowa y=x2+bx+c jest malejąca dla x∈(−∞;2⟩ a zbiorem jej wartości jest przedział ⟨−4;∞) . Postać kanoniczna tej funkcji opisana jest wzorem
A. f(x)=(x−2)2−4
B. f(x)=(x+2)2+4
C. f(x)=(x+4)2+2
D. f(x)=(x−4)2+2
Matura 2017
Zadanie 5. (1 pkt)
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział (−∞;3⟩ .
A. f(x)=−(x−2)2+3
B. f(x)=(2−x)2+3
C. f(x)=−(x+2)2−3
D. f(x)=(2−x)2−3
Matura 2017
Zadanie 6. (1 pkt)
Zbiorem wartości funkcji kwadratowej f(x)=−13x2−2x+c jest przedział (−∞,7⟩ . Zatem współczynnik c jest równy
A. −3
B. 4
C. 7
D. 10
Matura 2017
Zadanie 7. (1 pkt)
Wskaż funkcję kwadratową, której zbiorem wartości jest przedział ⟨−2,∞) .
A. y=−2x2+2
B. y=−(x+1)2−2
C. y=2(x−1)2+2
D. y=(x+1)2−2
Matura 2017
Zadanie 8. (2 pkt)
Wykresem funkcji kwadratowej f(x)=2x2+bx+c jest parabola, której wierzchołkiem jest punkt W=(4,0) . Oblicz wartości współczynników b i c .
Matura 2017
Zadanie 9. (1 pkt)
W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie A=(2,4) , która jest wykresem funkcji kwadratowej f .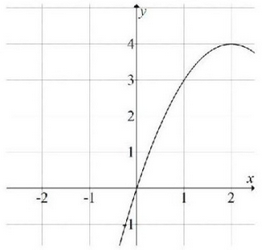 
Funkcja f może być opisana wzorem
Funkcja A. f(x)=(x−2)2+4
B. f(x)=(x+2)2+4
C. f(x)=−(x−2)2+4
D. f(x)=−(x+2)2+4
Matura 2017
Zadanie 10. (5 pkt)
Funkcja kwadratowa f określona jest wzorem f(x)=ax2+bx+c . Zbiorem rozwiązań nierówności f(x)>0 jest przedział (0,12) . Największa wartość funkcji f jest równa 9 . Oblicz współczynniki a , b i c funkcji f .
Matura 2017
Zadanie 11. (4 pkt)
Wyznacz wzór funkcji kwadratowej f w postaci ogólnej, wiedząc, że zbiorem wartości tej funkcji jest przedział (−∞,−1⟩ , a wartość −5 osiąga ona dla dwóch argumentów: 2 i 10 .
Matura 2017
Zadanie 12. (4 pkt)
Na rysunku są przedstawione fragmenty wykresów funkcji kwadratowych f i g . Funkcja f jest określona wzorem f(x)=−x2+6x−5 , a mniejsze z jej miejsc zerowych jest jednocześnie miejscem zerowym funkcji g . Wierzchołek W paraboli, która jest wykresem funkcji f , leży na wykresie funkcji g , a wierzchołek Z paraboli będącej wykresem funkcji g leży na osi Oy układu współrzędnych. Wyznacz wzór funkcji g . 
Matura 2017