Idź do:
2
4
6
8
10
12
Matura podstawowa - kurs - część 29 - zadania
Zadanie 1. (1 pkt)
Jaka jest najmniejsza wartość funkcji kwadratowej f(x)=x2+4x−3 w przedziale ⟨0,3⟩ ?
A. −7
B. −4
C. −3
D. −2
Odpowiedź: C
Matura 2017
Zadanie 2. (2 pkt)
Oblicz najmniejszą wartość funkcji kwadratowej f(x)=x2−6x+1 w przedziale ⟨0,1⟩ .
Odpowiedź: \(-4\)
Matura 2017
Zadanie 3. (2 pkt)
Oblicz największą wartość funkcji f(x)=−2x2+16x−15 w przedziale ⟨−2,3⟩ .
Odpowiedź: \(15\)
Matura 2017
Zadanie 4. (1 pkt)
Najmniejsza wartość funkcji f(x)=x2−3x+1 w przedziale ⟨−1,3⟩ jest równa
A. 5
B. 32
C. 1
D. −54
Odpowiedź: D
Matura 2017
Zadanie 5. (2 pkt)
Oblicz najmniejszą i największą wartość funkcji kwadratowej f(x)=x2−6x+3 w przedziale ⟨0,4⟩ .
Odpowiedź: \(f_{max}=3\) oraz \(f_{min}=-6\)
Matura 2017
Zadanie 6. (4 pkt)
Różnica największej i najmniejszej wartości, jakie funkcja kwadratowa f(x)=−12x2−2x+6 przyjmuje w przedziale ⟨−3,k⟩ dla k>0 jest równa 412 . Oblicz k .
Odpowiedź: \(k=1\)
Matura 2017
Zadanie 7. (4 pkt)
Wyznacz wartość największą funkcji f(x)=1x2+4x−1 w przedziale ⟨1,3⟩ .
Odpowiedź: \(\frac{1}{4}\)
Matura 2017
Zadanie 8. (4 pkt)
Największa wartość funkcji kwadratowej f(x)=a(x−2)2−4 , gdzie a≠0 , w przedziale domkniętym ⟨−4,−2⟩ jest równa 12 . Wyznacz najmniejszą wartość funkcji f w przedziale ⟨−4,−2⟩ .
Odpowiedź: \(\frac{28}{9}\)
Matura 2017
Zadanie 9. (2 pkt)
Najmniejszą wartością, jaką funkcja kwadratowa f dana wzorem f(x)=ax2+bx+c przyjmuje w przedziale ⟨0,4⟩ , jest f(2) . Uzasadnij, że a>0 i b<0 .
Matura 2017
Zadanie 10. (2 pkt)
Funkcja kwadratowa f przyjmuje w przedziale ⟨0,3⟩ największą wartość dla argumentów 0 i 3 . Uzasadnij, że w przedziale ⟨−2,5⟩ funkcja f przyjmuje największą wartość dla argumentów −2 i 5 .
Matura 2017
Zadanie 11. (1 pkt)
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej f . Wierzchołkiem tej paraboli jest punkt W=(1,9) . Liczby −2 i 4 to miejsca zerowe funkcji f .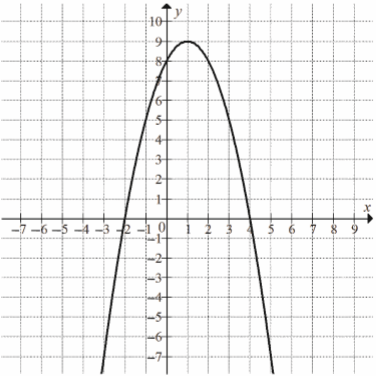 
Najmniejsza wartość funkcji f w przedziale ⟨−1;2⟩ jest równa
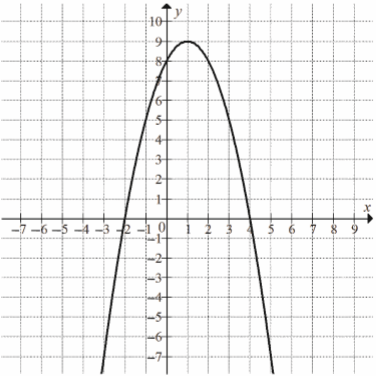Najmniejsza wartość funkcji A. 2
B. 5
C. 8
D. 9
Odpowiedź: B
Matura 2017
Zadanie 12. (2 pkt)
Funkcja kwadratowa jest określona wzorem f(x)=x2−11x . Oblicz najmniejszą wartość funkcji f w przedziale ⟨−6,6⟩ .
Odpowiedź: \(-30\frac{1}{4}\)
Matura 2017