Matura podstawowa - kurs - część 37 - zadania

W ciągu geometrycznym $(a_n)$ mamy $a_3 = 5$ i $a_4 = 15$. Wtedy wyraz $a_5$ jest równy.

Dany jest ciąg geometryczny $(a_n)$ , w którym $a_1=64$ i $q=-\frac{1}{2}$. Wówczas

Ciąg geometryczny $(a_n)$ określony jest wzorem $a_n=\frac{3^n}{4}$. Iloraz tego ciągu jest równy:

Ciąg geometryczny $(a_n)$ określony jest wzorem $a_n=-\frac{3^n}{4}$ dla $n\ge 1$. Iloraz tego ciągu jest równy

Dany jest ciąg geometyczny $(a_n)$, w którym $a_1=-\sqrt{2},\ a_2=2,\ a_3=-2\sqrt{2}$ . Dziesiąty wyraz tego ciągu, czyli $a_{10}$, jest równy

Liczby $64, x, 4$ są odpowiednio pierwszym, drugim i trzecim wyrazem malejącego ciągu geometrycznego. Oblicz piąty wyraz tego ciągu.

Ciąg $(27, 18, x+5)$ jest geometryczny. Wtedy

Trzeci wyraz ciągu geometrycznego równa się $45$, a szósty wynosi $1215$. Znajdź sumę ośmiu pierwszych wyrazów tego ciągu.

Ciąg geometryczny składa się z pięciu wyrazów, których suma wynosi $124$. Iloraz sumy wyrazów skrajnych przez wyraz środkowy równy jest $4{,}25$. Wyznacz ten ciąg.

Wyznacz rosnący ciąg geometryczny, wiedząc, że suma wyrazów skrajnych jest równa $34$, iloczyn tych wyrazów $64$, a suma wszystkich wyrazów ciągu wynosi $62$.

Jaką jednakową liczbę należy dodać do każdej z liczb $1, 10, 46,$ aby otrzymane sumy utworzyły ciąg geometryczny?

Liczby $3x−4$, $8$, $2$ w podanej kolejności są pierwszym, drugim i trzecim wyrazem ciągu geometrycznego. Wtedy

Nieskończony ciąg geometryczny $(a_n)$ jest określony wzorem $a_n=7\cdot 3^{n+1}$, dla $n\ge 1$. Oblicz iloraz $q$ tego ciągu.

Ciąg $(2x – 1, y, 6x + 3)\ $ jest arytmetyczny, a ciąg $(3, y, 27)\ $ jest geometryczny rosnący. Oblicz $x$ i $y$.

Liczby: $x-2,\ 6,\ 12$, w podanej kolejności, są trzema kolejnymi wyrazami ciągu geometrycznego. Liczba $x$ jest równa

W dziewięciowyrazowym ciągu geometrycznym o wyrazach dodatnich pierwszy wyraz jest równy $3$, a ostatni wyraz jest równy $12$. Piąty wyraz tego ciągu jest równy

Kwadrat $K_1$ ma bok długości $a$. Obok niego rysujemy kolejno kwadraty $K_2, K_3, K_4,...$ takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek). 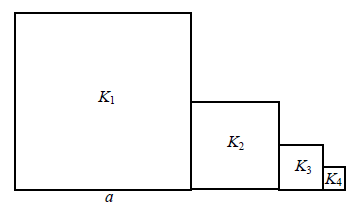Wyznacz pole kwadratu $K_{12}$.

Dany jest ciąg geometryczny $(a_n)$, w którym pierwszy wyraz jest równy $6$, a czwarty $12\sqrt{2}$. Liczba $\sqrt[3]{a_3-4}$ jest równa

Ciąg $(a_n)$ jest geometryczny oraz $a_1=2$, $a_2=6$. Liczby $a_3, x, \frac{x}{2}$ w podanej kolejności tworzą ciąg arytmetyczny. Oblicz $x$.

W rosnącym ciągu geometrycznym $(a_n)$, określonym dla $n\ge 1$, spełniony jest warunek $a_4=3a_1$. Iloraz $q$ tego ciągu jest równy