Idź do:
2
4
6
8
10
12
Matura podstawowa - kurs - część 43 - zadania
Zadanie 1. (1 pkt)
Kąt środkowy i kąt wpisany są oparte na tym samym łuku. Suma ich miar jest równa 180∘ . Jaka jest miara kąta środkowego?
A. 60∘
B. 90∘
C. 120∘
D. 135∘
Odpowiedź: C
Matura 2017
Zadanie 2. (1 pkt)
Punkty A,B,C,D dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego ACD jest równa 

A. 90∘
B. 60∘
C. 45∘
D. 30∘
Odpowiedź: C
Matura 2017
Zadanie 3. (2 pkt)
Punkty A i B leżą na okręgu o środku O i dzielą ten okrąg na dwa łuki, których stosunek długości jest równy 7:5 . Oblicz miarę kąta środkowego opartego na krótszym łuku. 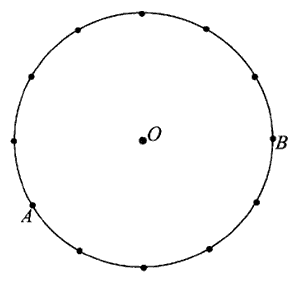

Odpowiedź: \(150^\circ \)
Matura 2017
Zadanie 4. (1 pkt)
Punkt O jest środkiem okręgu o średnicy AB (tak jak na rysunku). Kąt α ma miarę 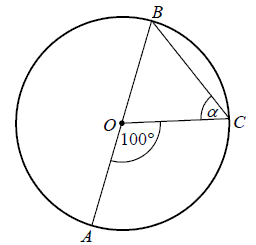

A. 40∘
B. 50∘
C. 60∘
D. 80∘
Odpowiedź: B
Matura 2017
Zadanie 5. (1 pkt)
Punkt O jest środkiem okręgu. Kąt α , zaznaczony na rysunku, ma miarę 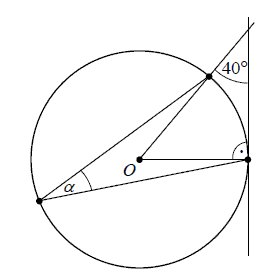

A. 50∘
B. 45∘
C. 25∘
D. 20∘
Odpowiedź: C
Matura 2017
Zadanie 6. (1 pkt)
Kąt środkowy oparty na łuku, którego długość jest równa 49 długości okręgu, ma miarę
A. 160∘
B. 80∘
C. 40∘
D. 20∘
Odpowiedź: A
Matura 2017
Zadanie 7. (1 pkt)
Punkty A , B i C leżą na okręgu o środku O (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy AOB ma miarę 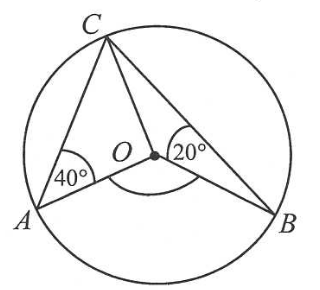

A. 60∘
B. 100∘
C. 120∘
D. 140∘
Odpowiedź: C
Matura 2017
Zadanie 8. (1 pkt)
Na okręgu o środku S leżą punkty A,B,C i D . Odcinek AB jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą AC jest równy 21∘ (zobacz rysunek). 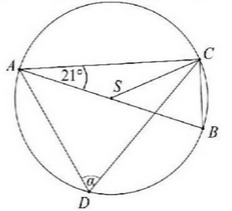 Kąt
Kąt α między cięciwami AD i CD jest równy
 Kąt
Kąt A. 21∘
B. 42∘
C. 48∘
D. 69∘
Odpowiedź: D
Matura 2017
Zadanie 9. (1 pkt)
Kąt ASB jest kątem środkowym w okręgu i jego miara wynosi 100∘ . Miara zaznaczonego kąta α jest równa 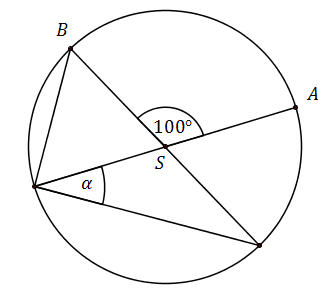

A. 40∘
B. 45∘
C. 50∘
D. 60∘
Odpowiedź: A
Matura 2017
Zadanie 10. (1 pkt)
Miara kąta wpisanego w okrąg jest o 20∘ mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A. 30∘
B. 20∘
C. 10∘
D. 5∘
Odpowiedź: B
Matura 2017
Zadanie 11. (1 pkt)
W okręgu o środku O dany jest kąt o mierze 50∘ , zaznaczony na rysunku. 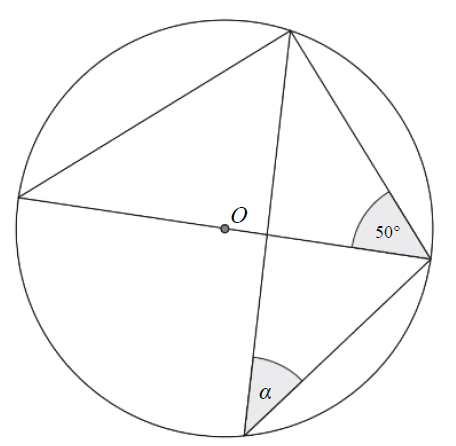 Miara kąta oznaczonego na rysunku literą
Miara kąta oznaczonego na rysunku literą α jest równa
 Miara kąta oznaczonego na rysunku literą
Miara kąta oznaczonego na rysunku literą A. 40∘
B. 50∘
C. 20∘
D. 25∘
Odpowiedź: A
Matura 2017
Zadanie 12. (2 pkt)
Punkty A , B , C , D są położone w tej kolejności na okręgu o środku O (zobacz rysunek). Odcinek DB jest średnicą tego okręgu i |∢BAC|=α , |∢CBD|=β . Wykaż, że α+β=90∘ . 

Matura 2017