Idź do:
1
2
3
4
5
6
7
8
Matura podstawowa - kurs - część 44 - zadania
Zadanie 1. (2 pkt)
Na odcinku AB wybrano punkt C , a następnie zbudowano trójkąty równoboczne ACD i CBE tak, że wierzchołki D i E leżą po tej samej stronie prostej AB . Okręgi opisane na tych trójkątach przecinają się w punktach C i P (zobacz rysunek). 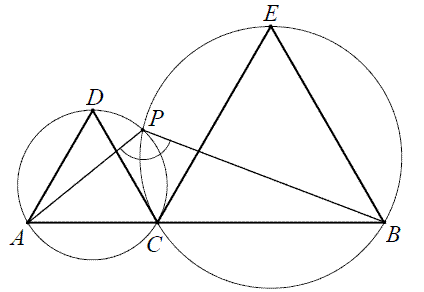 Udowodnij, że miara kąta
Udowodnij, że miara kąta APB jest równa 120∘ .
 Udowodnij, że miara kąta
Udowodnij, że miara kąta Matura 2017
Zadanie 2. (1 pkt)
Punkty A,B,C,D i E leżą na okręgu o środku S i dzielą ten okrąg na pięć łuków równej długości (zobacz rysunek). 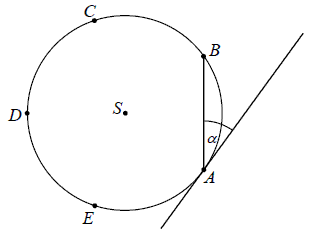 Wówczas miara kąta ostrego
Wówczas miara kąta ostrego α między cięciwą AB i styczną do tego okręgu w punkcie A jest równa
 Wówczas miara kąta ostrego
Wówczas miara kąta ostrego A. α=18∘
B. α=30∘
C. α=36∘
D. α=54∘
Odpowiedź: C
Matura 2017
Zadanie 3. (1 pkt)
Dane są dwa okręgi o promieniach 12 i 17 . Mniejszy okrąg przechodzi przez środek większego okręgu. Odległość między środkami tych okręgów jest równa
A. 5
B. 12
C. 17
D. 29
Odpowiedź: B
Matura 2017
Zadanie 4. (2 pkt)
Oblicz kąt α między cięciwą PQ , a styczną do okręgu w punkcie P . 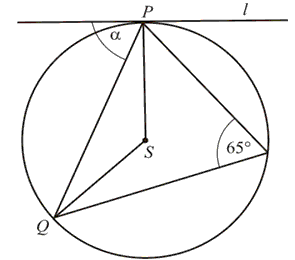

Odpowiedź: \(\alpha =65^\circ \)
Matura 2017
Zadanie 5. (2 pkt)
Dany jest prostokąt ABCD . Okręgi o średnicach AB i AD przecinają się w punktach A i P (zobacz rysunek). Wykaż, że punkty B,P i D leżą na jednej prostej. 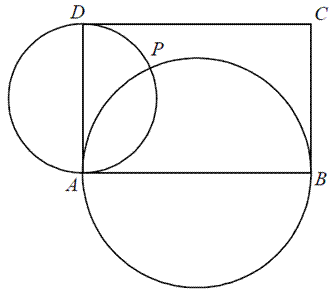

Matura 2017
Zadanie 6. (2 pkt)
Dwa okręgi są styczne zewnętrznie. Odległość ich środków jest równa 8 cm. Gdyby te okręgi były styczne wewnętrznie, to odległość ich środków byłaby równa 2 cm. Oblicz długości promieni tych okręgów.
Odpowiedź: \(r_1=5\), \(r_2=3\)
Matura 2017
Zadanie 7. (1 pkt)
Na trójkącie równoramiennym ABC , w którym |AC|=|BC| opisano okrąg o środku O . Prosta k jest styczna do tego okręgu w punkcie B i |∢BOC|=140∘ . 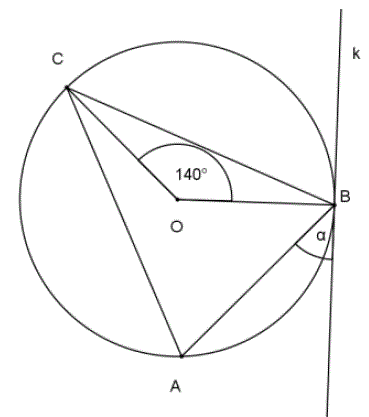 Kąt
Kąt α ma miarę
 Kąt
Kąt A. 70∘
B. 40∘
C. 90∘
D. 50∘
Odpowiedź: B
Matura 2017
Zadanie 8. (4 pkt)
Dwa okręgi o promieniach r i R są styczne zewnętrznie i są styczne do wspólnej prostej w punktach A i B (zobacz rysunek). Oblicz wartość iloczynu rR , jeżeli wiadomo, że odcinek AB ma długość 5 . 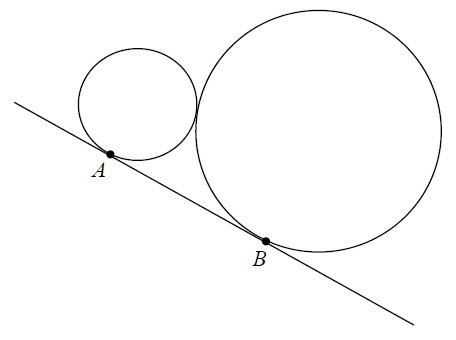
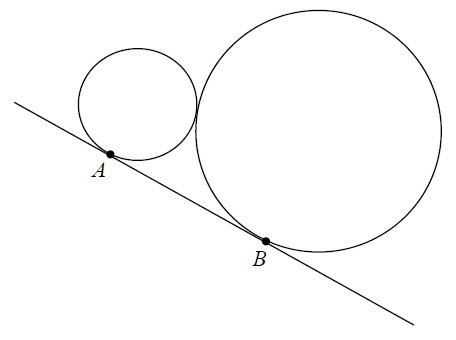
Odpowiedź: \(\frac{25}{4}\)
Matura 2017