Idź do:
1
2
3
4
5
6
7
8
9
Matura podstawowa - kurs - część 45 - zadania
Zadanie 1. (1 pkt)
Długość odcinka AB , równoległego do odcinka CD , jest równa 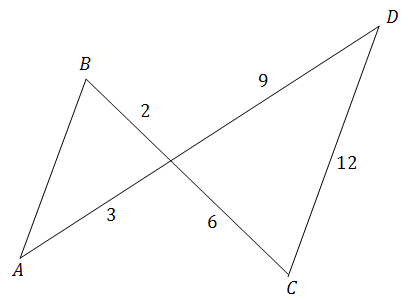

A. 6
B. 3
C. 2
D. 4
Odpowiedź: D
Matura 2017
Zadanie 2. (4 pkt)
Trójkąty prostokątne ABC i DEF są podobne. Przyprostokątne trójkąta ABC mają długości 5 i 12 , a przeciwprostokątna trójkątaDEF ma długość 26 . Wyznacz pole trójkąta DEF .
Odpowiedź: \(P=120\)
Matura 2017
Zadanie 3. (1 pkt)
Jeżeli trójkąty ABC i A′B′C′ są podobne, a ich pola są, odpowiednio, równe 25 cm2 i 50 cm2, to skala podobieństwa A′B′AB jest równa
A. 2
B. 12
C. 2–√
D. 2–√2
Odpowiedź: C
Matura 2017
Zadanie 4. (1 pkt)
Odcinki BC i DE są równoległe i |AE|=4 , |DE|=3 (zobacz rysunek). Punkt D jest środkiem odcinka AB . Długość odcinka BC jest równa 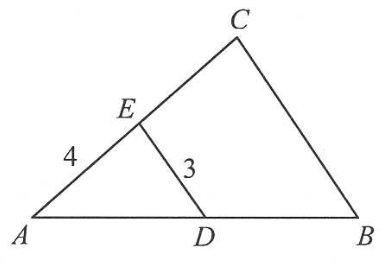

A. 4
B. 6
C. 8
D. 16
Odpowiedź: B
Matura 2017
Zadanie 5. (1 pkt)
Przedstawione na rysunku trójkąty są podobne.  Wówczas
Wówczas
 Wówczas
Wówczas A. a=13 , b=17
B. a=10 , b=18
C. a=9 , b=19
D. a=11 , b=13
Odpowiedź: B
Zadanie 6. (1 pkt)
Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku 1:4 , mogą być równe
A. 9 i 36
B. 18 i 36
C. 9 i 144
D. 18 i 144
Odpowiedź: B
Matura 2017
Zadanie 7. (5 pkt)
Pole trójkąta ABC równe jest S . Każdy bok trójkąta podzielono w stosunku x:y:x , gdzie x i y są pewnymi liczbami dodatnimi. Wyznacz pole sześciokąta, którego wierzchołkami są punkty podziałów boków trójkąta (zobacz rysunek). 

Odpowiedź: \(S\left (1-3\left (\frac{x}{2x+y}\right )^2\right )\)
Matura 2017
Zadanie 8. (2 pkt)
Odcinki AD i BE przecinają się w punkcie C . W trójkątach ABC i CDE zachodzą związki: |∢CAB|=|∢CED| , |AC|=5 , |BC|=3 , |CE|=10 (zobacz rysunek). Wykaż, że trójkąty ABC i CDE są podobne. Oblicz długość boku CD . 

Odpowiedź: \(6\)
Matura 2017
Zadanie 9. (2 pkt)
W trójkącie ABC punkt D jest środkiem boku AB oraz |CD|=|CB| (zobacz rysunek). Bok CB przedłużono tak, że |CB|=|BE| . Wykaż, że |AC|=|DE| . 

Matura 2017