Idź do:
2
4
6
8
10
12
14
Matura podstawowa - kurs - część 55 - zadania
Zadanie 1. (1 pkt)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa 6 , a kąt nachylenia jego przekątnej do płaszczyzny podstawy jest równy 60∘ . Długość tej przekątnej jest równa
A. 3
B. 3–√
C. 23–√
D. 43–√
Matura 2017
Zadanie 2. (4 pkt)
W ostrosłupie prawidłowym czworokątnym ABCDS o podstawie ABCD i wierzchołku S trójkąt ACS jest równoboczny i ma bok długości 8 . Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek). 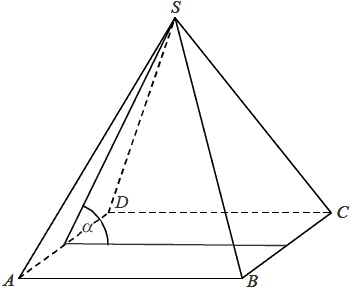

Matura 2017
Zadanie 3. (4 pkt)
W graniastosłupie prawidłowym czworokątnym ABCDEFGH przekątna AC podstawy ma długość 4 . Kąt ACE jest równy 60∘ . Oblicz objętość ostrosłupa ABCDE przedstawionego na poniższym rysunku. 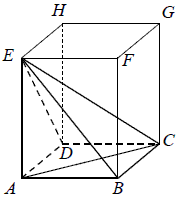

Matura 2017
Zadanie 4. (1 pkt)
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 5 cm, a krawędź podstawy 8–√ cm. Wówczas cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy:
A. 2–√5
B. 0,6
C. 0,4
D. 8–√10
Matura 2017
Zadanie 5. (5 pkt)
W graniastosłupie prawidłowym czworokątnym wysokość graniastosłupa jest o 4 krótsza od przekątnej podstawy i o 8 krótsza od przekątnej graniastosłupa. Oblicz sinus kąta pomiędzy przekątną graniastosłupa a płaszczyzną podstawy.
Matura 2017
Zadanie 6. (5 pkt)
W graniastosłupie prawidłowym czworokątnym ABCDEFGH połączono punkty będące środkami krawędzi BC , CD , AD i GH . Wyznacz objętość powstałej bryły wiedząc, że |DB|=52–√ i kąt DBH ma miarę 60∘ .
Matura 2017
Zadanie 7. (1 pkt)
W graniastosłupie prawidłowym czworokątnym EFGHIJKL wierzchołki E,G,L połączono odcinkami (tak jak na rysunku). 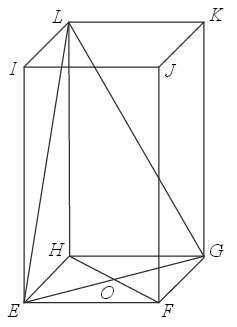 Wskaż kąt między wysokością
Wskaż kąt między wysokością OL trójkąta EGL i płaszczyzną podstawy tego graniastosłupa.
 Wskaż kąt między wysokością
Wskaż kąt między wysokością A. ∢OGL
B. ∢HOL
C. ∢HLO
D. ∢OHL
Matura 2017
Zadanie 8. (4 pkt)
Wysokość graniastosłupa prawidłowego czworokątnego jest równa 16 . Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego cosinus jest równy 35 . Oblicz pole powierzchni całkowitej tego graniastosłupa.
Matura 2017
Zadanie 9. (1 pkt)
Pole podstawy graniastosłupa prawidłowego czworokątnego jest równe 36 , a miara kąta nachylenia przekątnej graniastosłupa do płaszczyzny jego podstawy jest równa 30∘ . Wysokość tego graniastosłupa jest równa
A. 32–√
B. 62–√
C. 26–√
D. 36–√
Matura 2017
Zadanie 10. (5 pkt)
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem 60∘ . Odległość spodka wysokości ostrosłupa od krawędzi jest równa 4 . Oblicz objętość tego ostrosłupa.
Matura 2017
Zadanie 11. (4 pkt)
Objętość ostrosłupa prawidłowego trójkątnego ABCS (tak jak na rysunku) jest równa 72 , a promień okręgu wpisanego w podstawę ABC tego ostrosłupa jest równy 2 . Oblicz tangens kąta między wysokością tego ostrosłupa i jego ścianą boczną. 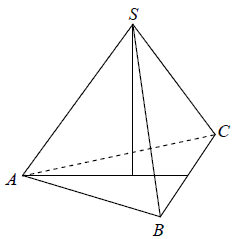

Matura 2017
Zadanie 12. (5 pkt)
Podstawą ostrosłupa ABCDS jest kwadrat ABCD . Wysokość SE ściany bocznej ADS jest jednocześnie wysokością ostrosłupa, a punkt E jest środkiem krawędzi AD (zobacz rysunek). Pole ściany ADS jest równe 12 cm2, a objętość ostrosłupa jest równa 48 cm3. Oblicz miarę kąta nachylenia krawędzi bocznej CS do płaszczyzny podstawy ostrosłupa. Wynik zaokrąglij do 1∘ . 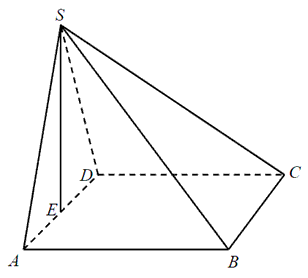

Matura 2017
Zadanie 13. (4 pkt)
Podstawą ostrosłupa ABCDS jest romb ABCD o boku długości 4 . Kąt ABC rombu ma miarę 120∘ oraz |AS|=|CS|=10 i |BS|=|DS| . Oblicz sinus kąta nachylenia krawędzi BS do płaszczyzny podstawy ostrosłupa.
Matura 2017
Zadanie 14. (4 pkt)
Podstawą ostrosłupa ABCDS jest prostokąt, którego boki pozostają w stosunku 3:4 , a pole jest równe 192 (zobacz rysunek). Punkt E jest wyznaczony przez przecinające się przekątne podstawy, a odcinek SE jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30∘ . Oblicz objętość ostrosłupa. 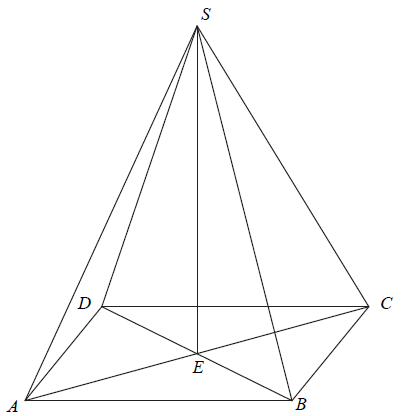

Matura 2017